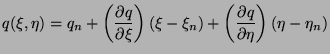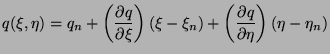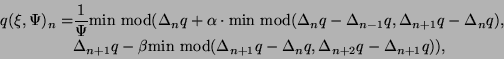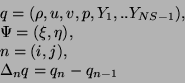Next: Schemat niejawny
Up: Całkowanie numeryczne równań podstawowych
Previous: Całkowanie numeryczne równań podstawowych
Spis treści
Schemat jawny zastosowany w pakiecie MultiFlower ma postać:
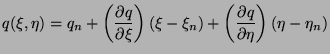 |
(3.6) |
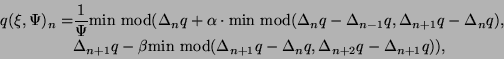 |
(3.7) |
gdzie:
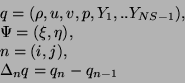 |
(3.8) |
Rodzaj schematu okreslają stałe
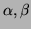 :
:
Tomasz Ochrymiuk
2000-07-07