



Next: Modyfikacje członów źródłowych w
Up: Człony źródłowe
Previous: Udział molowy
Spis treści
3.4
Zakładamy, iż proces spalania opisują elementarne reakcje chemiczne
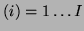 , zachodzące pomiędzy k-tymi składnikami. Każda z elementarnych reakcji ma
standardową dla gazów postać:
, zachodzące pomiędzy k-tymi składnikami. Każda z elementarnych reakcji ma
standardową dla gazów postać:
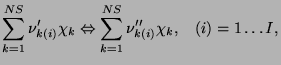 |
(3.20) |
gdzie: 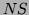 ilość składników chemicznych oznaczonych symbolem
ilość składników chemicznych oznaczonych symbolem 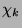 .
Współczynniki macierzy stechiometrycznych
.
Współczynniki macierzy stechiometrycznych
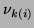 są liczbami całkowitymi
:
są liczbami całkowitymi
:
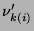 jest współczynnikiem k-tego składnika dla
postępującej i-tej reakcji, o wartości niedodatniej; natomiast
jest współczynnikiem k-tego składnika dla
postępującej i-tej reakcji, o wartości niedodatniej; natomiast
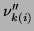 jest współczynnikiem stechiometrycznym dla odwrotnej reakcji o wartości nieujemnej.
Zazwyczaj elementarne reakcje zawierają tylko trzy, lub cztery składniki, stąd macierze
jest współczynnikiem stechiometrycznym dla odwrotnej reakcji o wartości nieujemnej.
Zazwyczaj elementarne reakcje zawierają tylko trzy, lub cztery składniki, stąd macierze
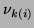 są ``rzadkie'' dla większości reakcji.
Szybkość produkcji składnika
są ``rzadkie'' dla większości reakcji.
Szybkość produkcji składnika
![$ \dot{\omega}_{k}\;\left[\frac{mol}{cm^{3}s}\right]$](img52.png) zależy od wszystkich reakcji zachodzących w danej chwili, stąd też jest równa:
zależy od wszystkich reakcji zachodzących w danej chwili, stąd też jest równa:
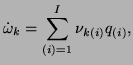 |
(3.21) |
gdzie: całkowity współczynnik stechiometryczny wynosi
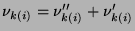 zaś
zaś
![$ q_{i}\;\;\left[\frac{mol}{cm^{3}s}\right]$](img55.png) jest stopniem zaawansowania
i-tej reakcji chemicznej, określonym następującą ogólną formułą reakcji chemicznych
jest stopniem zaawansowania
i-tej reakcji chemicznej, określonym następującą ogólną formułą reakcji chemicznych
![$\displaystyle q_{i}=k_{(i)}^{f}\prod_{k=1}^{NS}[X_{k}]^{\left\vert\nu_{k(i)}^{\...
...)}^{r}\prod_{k=1}^{NS}[X_{k}]^{\left\vert\nu_{k(i)}^{\prime\prime}\right\vert}.$](img56.png) |
(3.22) |
Tutaj ![$ [X_{k}]$](img42.png) (w
(w
![$ \left[\frac{mol}{cm^{3}}\right]$](img43.png) ) jest koncentracją
molową k-tego składnika,
) jest koncentracją
molową k-tego składnika,
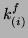 ,
,
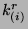 są współczynnikami
postępu i cofania się reakcji chemicznej. Współczynnik postępu dla (i)-tej
reakcji ma następującą postać Arrheniusa
są współczynnikami
postępu i cofania się reakcji chemicznej. Współczynnik postępu dla (i)-tej
reakcji ma następującą postać Arrheniusa
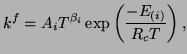 |
(3.23) |
w której bezwymiarowy współczynnik 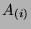 , wykładnik temperatury
, wykładnik temperatury
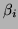 oraz energia aktywacji
oraz energia aktywacji
![$ E_{(i)}\;\left[\frac{cal}{mol}\right]$](img62.png) muszą być określone, jako dane specyfikujące reakcje chemiczne.
Stałe postępu reakcji zwrotnych
muszą być określone, jako dane specyfikujące reakcje chemiczne.
Stałe postępu reakcji zwrotnych
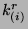 są, w ogólności,
związane ze stałymi
są, w ogólności,
związane ze stałymi
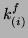 poprzez tzw. stałą równowagowej koncentracji
poprzez tzw. stałą równowagowej koncentracji
 -tej reakcji
-tej reakcji
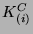
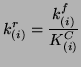 |
(3.24) |
która określona jest następującym domknięciem
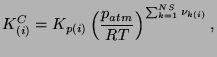 |
(3.25) |
gdzie
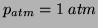 zaś stałe równowagowe
zaś stałe równowagowe 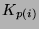 wynoszą
3.5
wynoszą
3.5
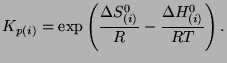 |
(3.26) |
Znak  odnosi się do zmiany jaka zachodzi w pełnym przejściu między składnikami
odnosi się do zmiany jaka zachodzi w pełnym przejściu między składnikami
 -tej reakcji a jej produktami. W szczególności, zmiany entropii
-tej reakcji a jej produktami. W szczególności, zmiany entropii
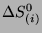 i
entalpii
i
entalpii
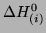 są obliczane jako:
są obliczane jako:
 |
(3.27) |
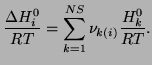 |
(3.28) |




Next: Modyfikacje członów źródłowych w
Up: Człony źródłowe
Previous: Udział molowy
Spis treści
Tomasz Ochrymiuk
2000-07-07
![]() , zachodzące pomiędzy k-tymi składnikami. Każda z elementarnych reakcji ma
standardową dla gazów postać:
, zachodzące pomiędzy k-tymi składnikami. Każda z elementarnych reakcji ma
standardową dla gazów postać: